ページ内リンク
熱伝導・熱伝導率 P74~P75(P74~P75)
三つの熱移動が基本です。「熱伝導」「対流熱伝達」「放射伝熱」
「熱伝導」と「熱伝達」の違いを把握すべし。<9次:P74 (6.1.1 熱伝導) >から<9次:P75 (6.1.2 熱伝達) >へと読み進みイメージを作りましょう。
近年(2019(R1)/12/21記ス)、数式の意味を問う問題がチラホラと出題される。式をザッと覚えて意味も把握したほうが良いだろう。熱伝導と熱伝達のどちらの頁に組み込もうか迷う問題があるのだが…、ま、そういうことで健闘を祈る。
テキスト9次改訂版について
『上級 受検テキスト:日本冷凍空調学会』9次改訂版(令和4年11月8日改訂)に対応しています。適当に、8次改訂版のページを( )内に残してあります。
フーリエの法則 P74
「フーリエの法則」が出題されるので、簡単に記しておく。テキスト<9次:P74左下 (6.1)式>
熱伝導(平板)説明図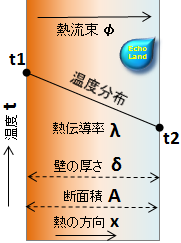
単位時間あたりの熱量(熱流束φ)は次式で成り立つ。(フーリエの法則)
φ = -λ(dt / dx) (kW/m2)
伝熱量Φは、
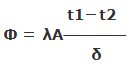 (kW)
(kW)
次ページの「ニュートンの冷却則」と混同させる問題が出題されるので注意すること。
・固体内を熱エネルギーが伝わる熱伝導においては、熱の流れる方向をx方向とし、ある位置xでの物体の温度をt、x方向への熱流束をφとすると、φ=λ(dt/dx)の関係がある。これをニュートンの冷却則といい、比例定数のλを熱伝導率という。 H29学/04 
【×】 正しい文章にしてみましょう。
固体内を熱エネルギーが伝わる熱伝導においては、熱の流れる方向をx方向とし、ある位置xでの物体の温度をt、x方向への熱流束をφとすると、φ = -λ(dt/dx)の関係がある。これをフーリエの法則といい、比例定数のλを熱伝導率という。
( - 記号を付けること。)
テキストは<9次(8次):P74左 (6.1.1 熱伝導)>の冒頭部分。「ニュートンの冷却則」は熱伝達の法則です。(テキスト<9次(8次):P75右真ん中辺り>
この問題は、下の「熱伝導率λ」にも掲載しておきます。
熱伝導
他の熱移動をからませてきますので、よく勉強しよく読みましょう。
・固体壁面と流動流体との間の熱移動を熱伝導という。 H20学/04 
【×】 この問題はココに置く。
対流熱伝達のことだね、<9次(8次):P75左下 (6.1.2 熱伝達)>の冒頭部分に記されている。
固体壁面とか流動流体とか言葉を記憶するだけじゃなくて、頭の中でイメージできるようにしよう。熱伝導については前ページ、物体内の熱移動。
・物体を通して熱エネルギーが伝わる熱移動現象を熱伝達という。 H20学/04 
【×】 この問題もココに置く。ぅん。これは熱伝導のことだよね。
熱伝達は流動流体と固体壁面都の間の移動。…3つの熱の移動をがっちり記憶すること。
・単位時間に移動する熱量を伝熱量という。熱流束は、単位面積当たりの伝熱量である。 R02学/04 
【◯】 この問題はココでよいだろう。
単位面積あたりの伝熱量φは上記の「フーリエの法則」の基本単位ですね。テキストは<9次(8次):P74 (6.1.1 熱伝導)>の冒頭から記されている。
熱伝導率λ
近年、同類問題が増えたので分類し新設しました。(2019(R1)/06/22)
・熱流束Φ、物体の温度t、熱の流れる方向をx方向とすると、φ=λ(dt/dx)の関係があり、比例定数のλを熱伝導率という。 H25学/04 
【×】 な、なんと! と、思う問題。
φ=-λ(dt/dx) ← 右辺に負の符号が付く。テキスト<9次(8次):P74左下2行目~>から引用しておきます。
なお、式(6.1)右辺の負の符号は、熱が流れる方向(x方向)に温度勾配(dt/dx)が常に負となるから、x方向の熱流束を正に表すために付けたものである。
なるほどね…。ってさ、これは、なんとも、ヤバイ問題だわ。
・固体内を熱エネルギーが伝わる熱伝導においては、熱の流れる方向をx方向とし、ある位置xでの物体の温度をt、x方向への熱流束をφとすると、φ=λ(dt/dx)の関係がある。これをニュートンの冷却則といい、比例定数のλを熱伝導率という。 H29学/04 
【×】 正しい文章にしてみましょう。
固体内を熱エネルギーが伝わる熱伝導においては、熱の流れる方向をx方向とし、ある位置xでの物体の温度をt、x方向への熱流束をφとすると、φ = -λ(dt/dx)の関係がある。これをフーリエの法則といい、比例定数のλを熱伝導率という。
( - 記号を付けること。)
 φ = -λ(dt / dx)
φ = -λ(dt / dx)
テキストは<9次(8次):P74左 (6.1.1 熱伝導)>の冒頭部分。「ニュートンの冷却則」は熱伝達の法則です。(テキスト<9次(8次):P75右真ん中辺り>
-λの負の符号は、熱が流れる方向(x方向)に温度勾配(dt/dx)が常に負となるから、x方向の熱流束を正に表すために付けるそうです。(テキスト<9次(8次):P74左一番下>)
・熱流速φ(kW/m^2)、物体の温度t(℃)、熱の流れる方向をx方向とすると、φ=-λ(dx/dt)の関係があり、比例定数のλを熱伝導率という。 H30学/04 
【×】 ぅ~ん、 φ = -λ(dt / dx)
この式を覚えておくしかないね。正しい文章にしておきましょう。
熱流速φ(kW/m^2)、物体の温度t(℃)、熱の流れる方向をx方向とすると、φ=-λ(dt/dx)の関係があり、比例定数のλを熱伝導率という。
・物体内を熱伝導によって一次元的に熱が伝わるとき、物体内の熱流束は温度勾配に比例し、その比例定数を熱伝導率という。このときの温度勾配は、熱が流れる方向に対して常に負となる。 R06学/04 
【◯】 😥 無勉の方はチンプンカンプンかもしれない。
テキスト<9次(8次):P74左下~>、熱流束式 φ=-λ(dx/dt)の、熱伝導率 λ と、 -(マイナス)符号の意味を、式を使わず文章で表した説明(問題文)です。フーリエの法則から始まる上記の過去問をこなしていれば把握できるでしょう。健闘を祈る。
円筒壁
近年、円筒壁の数式を問うものがポツリポツリと出題されたので分類し新設しました。(2019(R1)/12/21)
熱流束φ
テキスト<9次(8次):P74左 (6.1)式>
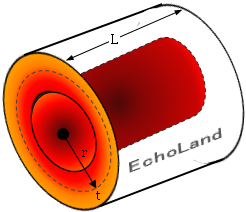
円筒壁の熱流束φ説明図
- 半径r方向にのみ一様に熱が流れている。
- 温度勾配(dt/dr)
- 熱伝導率λ
- 単位時間あたりの伝熱量Φ(kW)
- 円筒壁の長さL
- 熱流束φは、
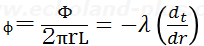 (kW/m2)
(kW/m2)
・平板の厚さ方向(x方向)にのみ、一様に熱が流れる場合、位置xにおける温度をtとすると、熱流束は温度勾配(dt/dx)に比例する。また、円筒壁を半径方向(r方向)にのみ、一様に熱が流れる場合、位置rにおける温度をtとすると、熱流束は温度勾配(dt/dr)に比例する。 R03学/04 
【◯】 この問題はココ。前半の「平板」は前述した「フーリエの法則」ですね、後半の「円筒壁」は上図を参照にしてちょうだい。(式の把握は必須になってます。)
・平板の熱流束φ(フーリエの法則)
φ = -λ(dt / dx) (kW/m2)
・円筒壁の熱流束φ
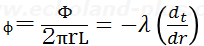 (kW/m2)
(kW/m2)
伝熱量Φ
テキスト<9次(8次):P75左 (6.4)式>
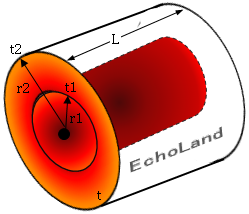
円筒壁の伝熱量説明用の図
- 円筒壁を半径方向( r 方向)にのみ一様に熱が流れる場合、円筒の内壁面(半径 r1 )および外壁面(半径 r2 )における温度をそれぞれ t1、t2とすると、半径 r が大きくなる方向への円筒壁の熱伝導による伝熱量 Φ は、(t1 - t2) / (ln r2 - ln r1)に比例する。
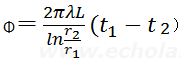 (kW)
(kW)
・円筒壁の熱伝導による伝熱量 Φ は、熱の流れる方向を半径 r が大きくなる方向とすると、(t1 - t2)/(ln r2 - ln r1)に比例する。ただし、内壁面を 1 、外壁面を 2 とする。 H25学/04 
【◯】 な、何これ、何、こ、この問題…。と、思う問題。
テキスト的には<9次(8次):P75左>の、式(6.4)辺りだけども、分からないワ。御愁傷様。
(学識の計算問題を2問確実にGET!しておかないと、こういう問題で点数が減っていくん(場合があるん)だワ。)ご健闘をお祈りします。
・円筒壁を半径方向( r 方向)にのみ一様に熱が流れる場合、円筒の内壁面(半径 r1)および外壁面(半径 r2)における温度をそれぞれ t1 、t2とすると、半径rが大きくなる方向への円筒壁の熱伝導による伝熱量Φは、(t1 - t2) / (ln r2 - ln r1)に比例する。 R01学/04 
【◯】 平成25年より6年後、テキスト<9次(8次:)P75左(6.4)式>が、
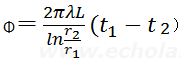 またもや出題された。1冷凍では実際に計算するだろうが、2冷の場合は式の意味を問われる。この先、このような問題が増えるのだろうか。健闘を祈る。(2019(R1)/12/21記ス)
またもや出題された。1冷凍では実際に計算するだろうが、2冷の場合は式の意味を問われる。この先、このような問題が増えるのだろうか。健闘を祈る。(2019(R1)/12/21記ス)
11/08/01 12/05/08 13/12/20 14/09/15 16/12/30 17/12/30 19/12/21 20/11/25 22/04/01 23/12/08 24/11/29
-- コラム --
修正・訂正箇所履歴
【2016/07/18 新設】(← 履歴をここに作った日)
- テキスト8次改訂版へ対応済み。解説見直し。(2016(H28)/12/31)
- 熱伝導率λを追加して問題を分類、及び、冒頭文章改編。(2019(R01)/06/22)
-
Φ=λ(dt/dx)
→φ=λ(dt/dx)
(2019(R01)/09/20) - 文章見直し。(2019(R01)/09/20)
- 「円筒壁の伝熱量」を追加。(2019(R01)/12/21)
- 令和元の円筒壁の問題(R01学/04)解説文の式が表示されていなかったので修正。(2020(R02)/03/10)
- 「フーリエの法則」を追加。解説文など文章見直し。(2020(R02)/11/25)
- 分割など全体的に見直し。(2022(R04)/04/01)
- 『上級 受検テキスト:日本冷凍空調学会』9次改訂版(令和4年11月8日改訂)に対応。(2023(R05)/09/17)
【参考文献・リンク】
- 初級 受検テキスト(SIによる初級受検テキスト):日本冷凍空調学会
- 上級 受検テキスト(SIによる上級受検テキスト):日本冷凍空調学会
- 冷凍機械責任者(1・2・3冷)試験問題と解答例(13):日本冷凍空調学会
- 第3種冷凍機械責任者試験模範解答集 :電気書院
- 第1・2種冷凍機械責任者試験模範解答集 :電気書院
