2台の蒸発器
平成22年度と同等の問題です。
第一種冷凍 令和4年度 問2 2台の蒸発器
問2 下図に示すアンモニアを冷媒とする蒸発温度の異なる2台の蒸発器を1台の圧縮機で冷却する冷凍装置が、下記の条件で運転されている。この装置について、次の(1)の問は解答用紙のp-h線頭上に、(2)および(3)の問は解答用紙の所定欄に計算式を示して答えよ。
ただし、圧縮機の機械的摩擦損失仕事は吐出しガスに熱として加わるものとする。また、配管での熱の出入りおよび圧力損失はないものとする。また、配管での熱の出入りおよび圧力損失はないものとする。
(20点)
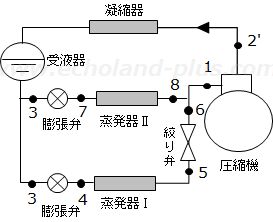
(運転条件)
圧縮機吸込み蒸気の比エンタルピー h1 = 1540 kJ/kg
圧縮機の断熱圧縮後の吐出しガスの比エンタルピー h2 = 1780 kJ/kg
膨張弁直前の液の比エンタルピー h3 = 280 kJ/kg
蒸発器Ⅰの出口冷媒の比エンタルピー h5 = 1580 kJ/kg
蒸発器Ⅱの出口冷媒の比エンタルピー h8 = 1480 kJ/kg
圧縮機のピストン押しのけ量 V = 270 m3/h
圧縮機吸込み蒸気の比体積 ν1 = 0.45 m3/kg
凝縮圧力 Pk における飽和液の比エンタルピー hkB = 345 kJ/kg
凝縮圧力 Pk における飽和蒸気の比エンタルピー hkD = 1485 kJ/kg
蒸発器Ⅰの蒸発圧力 Po1 における飽和液の比エンタルピー ho1B = 220 kJ/kg
蒸発器Ⅰの蒸発圧力 Po1 における飽和蒸気の比エンタルピー ho1D = 1470 kJ/kg
蒸発器Ⅱの蒸発圧力 Po2 における飽和液の比エンタルピー ho2B = 150 kJ/kg
蒸発器Ⅱの蒸発圧力 Po2 における飽和蒸気の比エンタルピー ho2D = 1450 kJ/kg
圧縮機の体積効率 ηv = 0.75
圧縮機の断熱効率 ηc = 0.70
圧縮機の機械効率 ηm = 0.85
(1) この冷凍装置の冷凍サイクルを、運転条件の数値を参照して解答用紙のp-h線図上に描き、点3 から点8 の各状態点を図中の適切な位置に記入せよ。ただし、点1 および点2' は、解答用紙のそれぞれの点を通るものとする。なお、点2'は実際の圧縮機の吐出しガス状態点を示す。
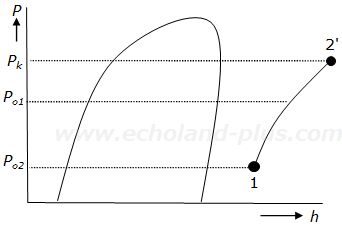
問(1)の解答用紙のp-h線図
(2) 蒸発器Ⅰの冷媒循環量 qmr1(kg/s)および蒸発器Ⅱの冷媒循環量 qmr2(kg/s)をそれぞれ求め、蒸発器Ⅰと蒸発器Ⅱの合計の実際の冷凍能力 Φo(kW)を求めよ(冷媒循環量は小数点以下第3位、冷凍能力は小数点以下第1位までとする)。
(3) この冷凍装置の実際の成績係数 COPR を求めよ。(成績係数は小数点以下第2位までとする)。
(1) この冷凍装置の冷凍サイクルを、運転条件の数値を参照して解答用紙のp-h線図上に描き、点3から点8の各状態点を図中の適切な位置に記入せよ。ただし、点1および点2'は、解答用紙のそれぞれの点を通るものとする。なお、点2'は実際の圧縮機の吐出しガス状態点を示す。
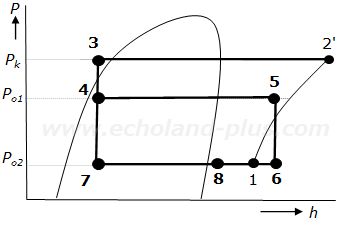
問(1)p-h線図の解答図(太線と太字を書き加える。)
この線図は、理屈は後回しにしてまず描くことができるようにしたい。
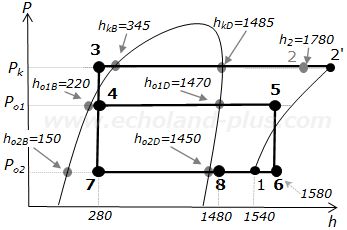
【参考】問(1)p-h線図の解答(比エンタルピー記入図)
設問には、各圧力の飽和線上の比エンタルピー値が記されている。p-h線図上の各状態点の記入位置の参考にしなさいということだろう。
(2) 蒸発器Ⅰの冷媒循環量 qmr1(kg/s)および蒸発器Ⅱの冷媒循環量 qmr2(kg/s)をそれぞれ求め、蒸発器Ⅰと蒸発器Ⅱの合計の実際の冷凍能力 Φo(kW)を求めよ(冷媒循環量は小数点以下第3位、冷凍能力は小数点以下第1位までとする)。
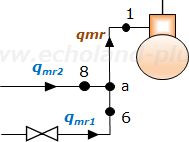
2台の蒸発器a点の熱収支解説概略図
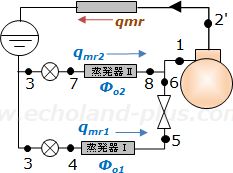
2台の蒸発器p-h線図 qmr 解説概略図
基本式 (参考です。本番では記述しなくてよいです。)
qmr = [(V/3600) ηv] / v1 …(1)
注)V/3600 単位変換する
qmr = qmr1 + qmr2 …(2)
a点の熱収支(左辺に出るもの、右辺に入るもの)
qmrh1 = qmr1h5 + qmr2h8 …(3)
Φo = Φo1 + Φo2
Φo1 = qmr1(h5 - h4))
Φo2 = qmr2(h8 - h7))
h5 = h6 h3 = h4 = h7
(1)式より、qmrを求めましょ。
qmr = [(V/3600) ηv] / v1
= [(270/3600) × 0.75] / 0.45
= 0.05625 / 0.45
= 0.125 (kg/s)
(2)式と(3)式より qmr1 、qmr2 を求めましょ。いままでの過去問では、h6 を求めたり、 qmr1 、qmr2 の比率が指定されていましたが、設問では比率指定はなし、比エンタルピーはすべて指定されています。少々戸惑いますが数学を解く感じでしょう。
(3)式に数値代入
qmrh1 = qmr1h5 + qmr2h8
0.125 × 1540 = 1580qmr1 + 1480qmr2 …(3-1)
まず、qmr1 を求めるため、(2)式に数値代入して変更。
qmr = qmr1 + qmr2
qmr2 = 0.125 - qmr1 …(2-1)
では、(3-1)式に(2-1)を代入。
0.125 × 1540 = 1580qmr1 + 1480qmr2 …(3-1)
192.5 = 1580qmr1 + 1480(0.125 - qmr1)
192.5 = 1580qmr1 + 185 - 1480qmr1)
192.5 = 185 + 100qmr1
192.5 - 185 = 100qmr1
qmr1 = 7.5 / 100 = 0.075 (kg/s)
qmr2は、
qmr2 = 0.125 - qmr1
= 0.125 - 0.075
= 0.050 (kg/s)
注)長々と数式を記述しましたが、本番では大胆に短縮してください!基本式と答えが合っていれば得点をもらえるでしょう。
ここに、蒸発器Ⅰの冷凍能力を Φo1、蒸発器Ⅱの冷凍能力をΦo2とする。
Φo1 = qmr1(h5 - h4)
= 0.075 × (1580 - 280)
= 0.075 × 1300
= 97.5 (kW)
Φo2 = qmr2(h8 - h7)
= 0.050 × (1480 - 280)
= 0.050 × 1200
= 60 (kW)
Φo = Φo1 + Φo2 = 97.5 + 60 = 157.5 (kW)
答え qmr1 = 0.075 (kg/s) qmr2 = 0.050 (kg/s) Φo = 157.5 (kW)
(3) この冷凍装置の実際の成績係数 (COP)R を求めよ。(成績係数は小数点以下第2位までとする)。
h'2 = h1 + (h2 - h1) / ηcηm
= 1540 + (1780 - 1540) / 0.70 × 0.85
= 1540 + 240 / 0.595
= 1943.36
(COP)R = Φo / P
= Φo / qmr(h'2 - h1)
= 157.5 / 0.125 × (1943.36 - 1540)
= 157.5 / 0.125 × 403.36
= 157.5 / 50.42 = 3.1237604
≒ 3.12
答え (COP)R = 3.12
この問題の要点は、
- 2台の蒸発器のp-h線図を描くことができるか
- 蒸発器Ⅰと蒸発器Ⅱの合流点a の熱収支式を組み立てられるか。
- 数学パズルを解くセンス?
いつもながらですが、計算はくどくどと記しています。本番では、思い切って削除しスマートな記述にしてください。それには、過去問をこなし これでどうだ!採点者殿!
と豪語するような自信を持てるぐらいになりましょう。
ご健闘をお祈りします。
訂正箇所履歴
【2023(R05/01/16 新設】
- 全般に見直し。(2026(R08)/02/24)