R407C用の高圧受液器として使用したい円筒胴圧力容器
昨年度と同等かな。
第一種冷凍機械責任者試験 令和3年度 問5(11月試験)
問5 下記仕様の鋼板がある。この鋼板を用いて、屋外に設置して凝縮温度50℃で運転されるR407C用高圧受液器を設計したい。この高圧受液器について、設計可能な最大の円筒胴の外径 Do(mm) を解答用紙の所定欄に計算式を示して整数値で求めよ。
ただし、溶接継手の効率は0.70、R407Cを冷媒とする冷凍装置の凝縮温度50℃ における高圧部設計圧力は2.11 Mpa とする。
また、この円筒胴に、溶接継手のない半球形鏡板を取り付け、この鏡板の内面に設計圧力2.11 Mpa が作用した場合、半球面の接線方向に誘起される引張応力 σt(N/mm2) を、解答用紙の所定欄に計算式を示して、小数点以下1桁まで求めよ。円筒胴と鏡板は外径寸法 Do(mm) を同一とする。
(20点)
(鋼板の仕様)
使用鋼板 SM400B
円筒胴に使用する鋼板の厚さ ta1 = 7 mm
鏡板に使用する鋼板の厚さ ta2 = 7 mm
設計可能な最大の円筒胴の外径 Do(mm) を求める。
- 腐れしろαは屋外設置なので、α = 1 とする。
- 許容引張応力σa はSM400B なので、σa=100 N/mm2 とする。
- 溶接効率は η とする。η = 0.70
- 円筒胴板厚 ta1 = 7 mm
- 設計圧力をPとする。 P = 2.11 Mpa
次式よりDi を求める。(参照:『上級 冷凍受験テキスト:日本冷凍空調学会』<9次:P179左 (12.8)式><8次:P172左 (12.8)式>)
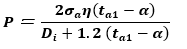
式の変形が面倒だなぁ…。本番では、変形過程は記述しなくても全然良いです。参考に書いておきます。
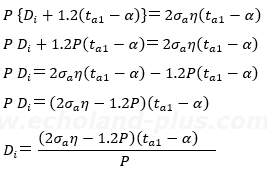
じゃ、数値代入しましょう。
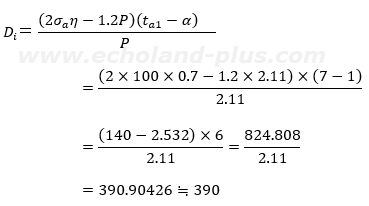
整数値指定なので、小数点以下は切り捨てる。(四捨五入して391とすると致命的間違い。0点かも。)
外径Do は、
Do = Di + 2ta1 = 390 + 2 × 7 = 404
答え Do = 404 mm
円筒胴に取り付ける半球面の接線方向に誘起される引張応力 σt(N/mm2) を求める。
与えられている数値は、
- 腐れしろ α = 1 mm
- 半球形形状に関する係数 W = 1
半球形鏡板は 1(参照:『上級 冷凍受験テキスト』<9次:P180左 3行目~><8次:P173右 (12.14)式の下>) - 鏡板は溶接継手がないので η = 1
- 鏡板の鋼板の厚さ ta2 = 7 mm
半球形鏡板の接線方向の引張応力 σt を求める式は、
(参照:テキスト<9次:P180左 (12.12)式><8次:P173右 (12.14)式>)
σt = PRW / 2t (N/mm2)
鏡板の半径R は、
R = Do - 2ta2 / 2 = 404 - 2 × 7 / 2 = 195 mm
よって、
σt = PRW / 2t = 2.11 × 195 × 1 / 2 × 7
= 29.389285 ≒ 29.4 (小数点以下2桁目を四捨五入)
答え σt = 29.4 (N/mm2)
この(令和3年度の)問題は、過去問をこなして公式を覚えれば大丈夫でしょう。
いつもながらですが、計算はくどくどと記しています。本番では、思い切って削除しスマートな記述にしてください。
ご健闘をお祈りします。
訂正箇所履歴
【2022(R04)/06/26 新設】
- 『上級 冷凍受験テキスト』9次改訂版に対応。(2023(R05)/08/10)