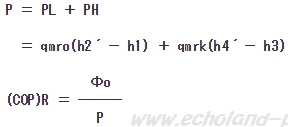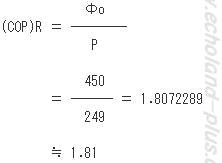二段圧縮一段膨張アンモニア冷凍装置
（実際の冷凍装置の運転条件）に「押しのけ量比」があるのを発見。おもわず、凹む。
第一種冷凍機械責任者試験 平成26年度（11月試験）
問1 下図のp-h線図で示す二段圧縮一段膨張によるアンモニア冷凍装置が下記の冷凍サイクルの運転条件で運転されているとき、次の(1)～(3)の間に、解答用紙の所定の欄に計算式を示して答えよ。
ただし、圧縮機の機械的摩擦損失仕事は吐出しガスに熱として加わるものとする。また、配管での熱の出入りおよび圧力損失はないものとする。
（20点）
（1）低段圧縮機の体積効率ηvLを求めよ。
（2）高段圧縮機の体積効率ηvHを求めよ。
（3）この冷凍装置の実際の成績係数(COP)Rを求めよ。
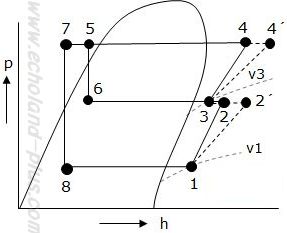
なにはともあれ、概略図と線図を描きましょう。
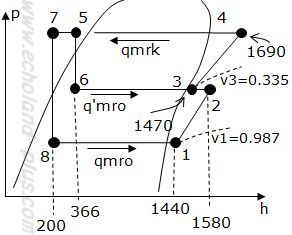
線図には数値を記入してみましょう。
概略図もスラスラリと描けるようにしましょう。
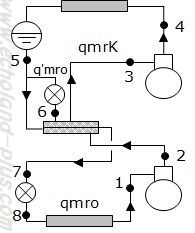
- Φo ＝ 450 kW
- VL ＝ 1500 m^3/h
- a ＝ 2.0
- 低・高段とも ηc ＝ 0.70
- 低・高段とも ηm ＝ 0.90
（1）低段圧縮機の体積効率ηvLを求めよ。
（1）式から
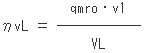※注）VLはm^3/hなので、m^3/sに換算すること。
この式で、不明なのはqmroです。求めましょう。
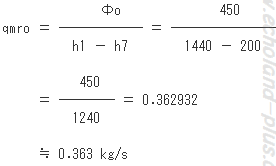
では、（1）の山頂へゴール
答え ηvL ＝ 0.86
（2）高段圧縮機の体積効率ηvHを求めよ。
（1）で使った式から、
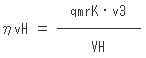
この式で、不明なのはqmrkと、VHです。この（2）が、この問1のポイントですね。
では、qmrkから求めましょう。ハイ、中間冷却器の熱収支の式を組み立ててみましょう！
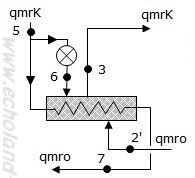
左辺に入るもの、右辺に出るものをまとめます。
qmrk・h5 ＋ qmro・h2´＝ qmrk・h3 ＋ qmro・h7
h2は、h2´であることに注意
qmroを左辺、qmrkを右辺にまとめます。
qmro・h2´－ qmro・h7 ＝ qmrk・h3 － qmrk・h5
qmro(h2´－ h7) ＝ qmrk(h3 － h5)
ハイ、qmroとqmrkを含んだ熱収支式の出来上がり。
さて、h2´を求めましょうかね。
では、qmrkを求めましょう。
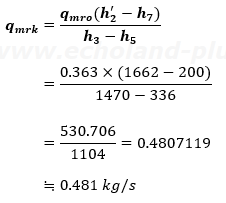
じゃ、VHを求めましょう。
押しのけ量の比 a ＝ 2.0 なので、
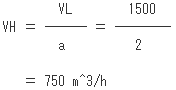
押しのけ量比とか見慣れない項目でしたが、一息入れたら、どうってことないですね。
では一気に、ηvHを求めますか。
3600で除して、VHをm^3/hから、m^3/sに変換を忘れないように。
答え ηvH ＝ 0.77
（3）この冷凍装置の実際の成績係数(COP)Rを求めよ。
チョッと、2通りの解き方を書いておきます。
成績係数(COP)Rを求める【その1】
基本式は、
ここで、h2´＝ 1662 kJ/kg
h4´は、
答え (COP)R ＝ 1.81
成績係数(COP)Rを求める【その2】
Pを一気に求めます。（これのほうが、スマート。）
基本式は、
答え (COP)R ＝ 1.81
当然、本番では、こんなに長々と式を書かないように。（実際、そんなに書くところがありません。）
ご健闘をお祈りしています。
訂正箇所履歴
【2016(H28)/02/11 新設】
- スマホなどで崩れる計算式などを、自動で大きさが変化する画像にした。（2017(H29)/04/25）
- 問題の運転条件「圧縮機の機械効率（低段側、高段側とも） ηm ＝ 0.70」←数値を誤植していたので修正。「ηm ＝ 0.90」（なお、解説部分は誤植なし。）（2018(H30)/02/17）
- (2)のqmrkの数値代入式で、h2´が1660に誤植 → 1662に修正。（2020(R02)/12/18）
- (2)のηvHを求める式（最後の数値代入の式）の分子「qvk・v3」 → 「qmrk」に修正。（2020(R02)/12/18）