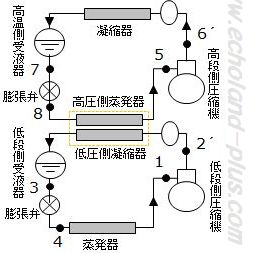
二元冷凍装置は初めての出題かな…。
手元の資料を平成4年までさかのぼっても二元冷凍装置の問題は見あたらない。（検定試験は不明）とってもレアな問題。
第一種冷凍機械責任者試験 平成24年度（11月試験）
問1 R404AとR23を冷媒とする二元冷凍装置を下図に示す。この装置を下記の冷凍サイクルの条件で運転するとき、次の(1)および (2)の間に、解答用紙の所定欄に計算式を示して答えよ。
ただし、圧縮機の機械的摩擦損失仕事は、熱として冷媒に加わらないものとする。また、配管での熱の出入りおよび圧力損失はないものとする。
（20点）
（1）低温側冷媒循環量qmro (kg/s)および高温側冷媒循環量qmrk (kg/s)を求めよ。
（2）実際の圧縮機の総軸動力P（kW）および実際の冷凍装置の成績係数（COP)Rを求めよ。
なお、計算式に必要なときは、次の記号を使用するものとする。
なにはともあれ、線図を描きましょう。
ηc ＝ 0.70
ηm ＝ 0.90
Φo ＝ 50 kW
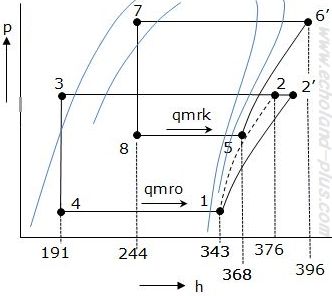
『上級 冷凍受験テキスト：日本冷凍空調学会』＜9次(8次)：P50 (図4.4 )＞の線図を参考に書いてみました。 はじめて書いたので結構時間がかかりました。イマイチ。（汗
（1）低温側冷媒循環量qmro (kg/s)および高温側冷媒循環量qmrk (kg/s)を求めよ。
はじめての二元なのでなんとなく戸惑いましたが、冷静に考えればどうってことないかも。
まずは、qmroからです。そうです！基本式はこれ。Φo ＝ qmro (h1 － h4)
ここに、h3 ＝ h4
なんとなく楽勝。さて、qmrkをどうやって求めるか…です。
『上級 冷凍受験テキスト』＜9次：P51 (4.16)式＞（＜8次：P50 (4.14)式＞）の熱収支の式を使うしかないでしょう。では、この公式を導いてみましょう。
「低圧側凝縮器」と「高圧側蒸発器」部分を抜き出してヒートバランスの式を組み立ててみましょう。
「出るものを左辺」「入るものを右辺」にまとめます。
qmrk・h5 ＋ qmro・h3 ＝ qmrk・h8 ＋ qmro・h2
まとめて、
qmrk（h5 － h8） ＝ qmro（h2 － h3）
そういうことで、テキストと同じ式が出来上がりました。記憶しなくてもこうしてヒートバランスの式を組み立てられれば鬼に金棒です。
さて、ここで「実際の」吐き出しガス比エンタルピーh2´を用いることに注意してください。
qmrk（h5 － h8） ＝ qmro（h2´ － h3） です。
h2´を求めましょう。
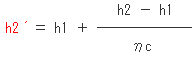
「機械的摩擦損失仕事は、熱として冷媒に加わらないものとする。」とあるので、ηmは入れずηcのみです。
じゃ、値を入れます。
では、qmrkを求めましよう。
答え 低温側冷媒循環量qmro ＝ 0.329 (kg/s) 高温側冷媒循環量qmrk ＝ 0.528 (kg/s)
実際の圧縮機の総軸動力P（kW）および実際の冷凍装置の成績係数（COP)Rを求めよ。
総軸動力Pは、二段膨張サイクルと同様に低段動力Poと高段動力Pkの和です。
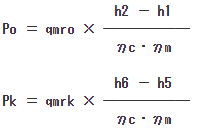P ＝ Po ＋ Pk
じゃ、数値を代入して一気に。
では一気にPと(COP)Pを求めましよう。
答え P ＝ 36.5（kW） (COP)R ＝ 1.37
そんなわけで、 とっても長い解答になってしまいましたが、本番ではこんなに書ききれません。採点者の気持ちになって要点が通じるような、ざっくりカットした計算式を組み立ててください。
二元冷凍装置は、二段圧縮二段膨張装置より簡単かもしれません。
ご健闘をお祈りしています。
訂正箇所履歴
【2016/02/11 新設】