1種冷凍学識計算攻略-問1：コンパウンド圧縮機攻略
EchoLand-plus
コンパウンド圧縮機も攻略し、問１をガッチリ固めよう！
コンパウンド圧縮機を用いた冷凍装置は、テキストによると設備が簡単なので普及しているようです。
コンパウンド圧縮機を用いた冷凍装置は、普通！？の二段圧縮冷凍装置と変わりありませんが、違うのは気筒数比が絡んできます。ま、数学的には 簡単な比の計算なんですけど…。
第一種冷凍機械責任者学識試験 平成17年度 問1
問1 下記仕様のR－22コンパウンド圧縮機を使用した二段圧縮一段膨張冷凍装置を、下記の理論冷凍サイクル条件で運転して120KWの冷凍能力を得たい。 これについて、次の(１)および(２)の間に、解答用紙の所定欄に計算式を示して答えよ。
ただし、圧縮機の機械的摩擦損失は吐出しガスに熱として加わるものとする。また、配管での熱の出入りはないものとする。 （20点）
（1）蒸発器の冷媒循環量qmL（kg/s）を求めよ。
（2）凝縮負荷Φk（kW）を求めよ。
ちなみに、前ページの平成18年講習検定試験問題1と数値がほとんど同じですね。ま、あまり深く考えなくてもいいんですけど。さて、なにわともあれ、概略図とp-h線図を書いてみましょう。
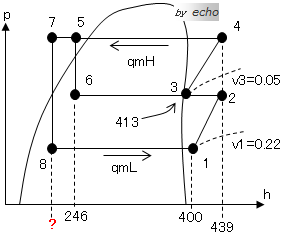
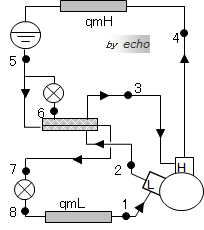
こんな感じになりました。低段側と高段側の圧縮機が一つになっている図です、あとの附属機器は前ページのものとまったく同じです。
（1）蒸発器の冷媒循環量qmL（kg/s）を求めよ。
頭のひねりどころです。
蒸発器の冷媒循環量qmLを求める場合は、冷凍能力Φoが120（kW）と指定されていますからこの公式で求められそうです。
Φo ＝ qmL（h1 － h8） …（1）
ところが、p-h線図の中に書いてありますがh8が？なのです。
この辺がこの問題のカギといいましょうか、コンパウンド圧縮機の気筒数比を使って答えを導き出すことができるか試される問題です。
気筒数比 a というのは、低段側と高段側のピストン押しのけ量の比です。 この辺は『上級 冷凍受験テキスト：日本冷凍空調学会』＜9次(8次)：P48 (4.2.3 コンパウンド圧縮機による二段圧縮冷凍装置)＞を勉強してください。
■ 気筒数比と冷媒循環量 ■
ピストン押しのけ量の計算式は、二種冷凍学識計算攻略のこのページ（別窓で開きます）で勉強しました。
この問題の低段側のピストン押しのけ量をVL、高段をVHとすると、
ぇ～と、気筒数比 a は、ピストン押しのけ量VLとVHの比ですから、
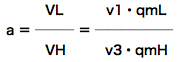（ηvは同じだから消えます）
ということは、
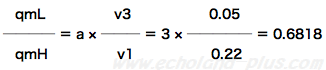…（2）
■ 冷媒循環量qmLとqmHの関係はもう一つ ■
さて、qmLとqmHの関係がもう一つあります。そうです、中間冷却器の熱収支です。さっそく、中間冷却器の図を書いてみましょう。もう簡単ですよね！？
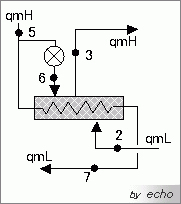
左辺に入るもの、右辺に出るものを書きます。
qmH・h5 ＋ qmL・h2´ ＝ qmH・h3 ＋ qmL・h7
まとめます
qmL(h2´－ h7) ＝ qmH(h3 － h5)
ここで、h2´を使っている事に注意してください。
よって、
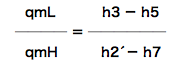…（3）
h2の実際の比エンタルピーh2´を求めましょう。
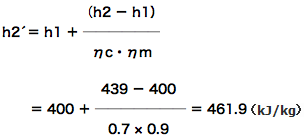
（2）と（3）式から
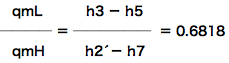…（4）
というわけで、熱収支からもqmLとqmHの比が導き出せました。ピストン押しのけ量と気筒数比から求めた比と同じ値、0.6818になりました。
ぅむ、h7が求めらますね。指定されている各比エンタルピー数値を入れます。
途中の計算は省いて、
h7 ＝ 216.96 （kJ/kg）
■ さぁ、待ちに待った!?（1）式を使いましょう。 ■
ここに、 h7 ＝ h8 …（5）
…（1）
指定された数値を代入します。
冷媒循環量は、下3桁（0.656）でよいですが、この場合は3桁以降が微妙な数字なので「0.6556」として下四桁にしておいたほうが良いです。次の凝縮負荷の答が微妙に変わってしまうからです。（その違いはここでは書きません、ぇ、面倒ですから…）
答え qmL ＝ 0.6556（kg/s）
（2）凝縮負荷Φk（kW）を求めよ。
さぁ、あとは怒濤のごとく片付けちゃいましょう。実際の比エンタルピー（h4´）を忘れないように。
h4の実際の比エンタルピーh4´を求めます。
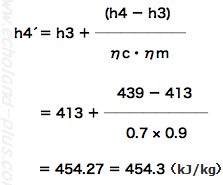
qmHを下記の（4）式と、（1）の問題の答え（qmL＝0.6556）から求めます。
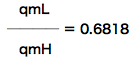…（4）
Φkは、
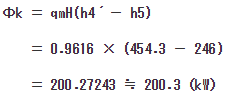
答え Φk ＝ 200.3(ｋW) めでたし、めでたし。
（1）、（2）まとめ
（1）
ピストン押しのけ量の高段側をVH、低段側をVLとすると、
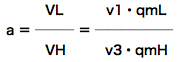
よって、
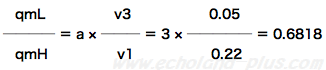-----（1）
h2の実際の比エンタルピーh2´は
-----（2）
中間冷却器の熱収支は、
qmH・h5 ＋ qmL・h2´ ＝ qmH・h3 ＋ qmL・h7
よって、
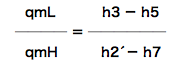
（1）、（2）式より
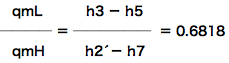
h7 ＝ 216.97
Φo ＝ qmL(h1 - h7)、 h7 ＝ h8 であるから、
答え 0.6556 （kg/s）
（2）
h4の実際の比エンタルピーh4´は
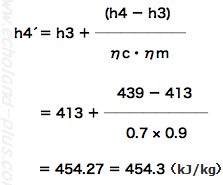
答え 200.3 （kW）
ちょっと、まだ長いですかね・・・。もっと、切りつめてしまっても良いかもしれません。
如何でしょうか、頭を少し柔らかくして、あっちからもこっちからも考えて解き方を探していく必要があります。 ま、問題を何度も解いているうちに、感と言いましょうか、なんと言いましょうか、とにかく分かってくると思います。
「中間冷却器の熱収支と実際の比エンタルピー」中間冷却器の熱収支の式を書く事ができるかどうか…、この辺がポイントです。過去問ガンガンやって、サクッとこなせるようにしましょう。
次ページに熱収支のまとめを書いておきます。二段圧縮の解き方はこの辺で終了。
もう一問ぐらい書こうかと思いましたが、いずれ追加することにします。 ← 過去問リストから勉強しましょう。
訂正箇所履歴
【2016/10/22 新設】
- 計算式がスマホなどで崩れるため、自動で大きさが変化する画像にした。解説文等も見直し。（2017/04/02）
- 『上級 冷凍受験テキスト』9次改訂版に対応。（2023(R05)/05/31）