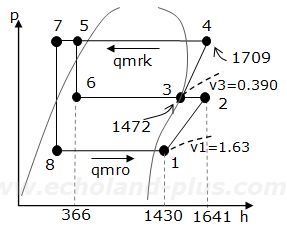
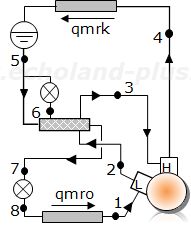
コンパウンド圧縮機二段圧縮一段膨張冷凍装置です。
令和2年度と同等のコンパウンド圧縮機の問題です。微妙に問うものが違いますが難問ではありません。気筒数比がポイントです。
第一種冷凍機械責任者試験 令和3年度（講習検定試験）
問1 下記仕様のコンパウンド圧縮機を使用したアンモニア二段圧縮一段膨張冷凍装置があり、
その理論冷凍サイクルは以下のとおりである。これについて、次の(1)～(4)に、それぞれ解答用紙に計算式を示して答えよ。
ただし、圧縮機の機械的摩擦損失仕事は熱となって冷媒に加わるものとし、機器および配管と周囲との間で熱の出入りはないものとする。（20点）
（理論冷凍サイクル）
高段側冷媒循環量 qmrk ＝ 0.5 kg/s
低段側吸込み蒸気の比エンタルピー h1 ＝ 1430 kJ/kg
低段側吸込み蒸気の比体積 v1 ＝ 1.63 m3/kg
理論断熱圧縮後の低段側吐出しガスの比エンタルピー h2 ＝ 1641 kJ/kg
高段側吸込み蒸気の比エンタルピー h3 ＝ 1472 kJ/kg
高段側吸込み蒸気の比体積 v3 ＝ 0.390 m3/kg
理論断熱圧縮後の高段側吐出しガスの比エンタルピー h4 ＝ 1709 kJ/kg
中間冷却器用膨張弁直前の冷媒液の比エンタルピー h5 ＝ 366 kJ/kg
（圧縮機仕様）
低段側と高段側の気筒数比 a ＝ 3
体積効率（低段側、高段側とも） ηv ＝ 0.75
断熱効率（低段側、高段側とも） ηc ＝ 0.70
機械効率（低段側、高段側とも） ηm ＝ 0.90
(1) 低段側冷媒循環量qmro(kg/s)と高段側冷媒循環量qmrk(kg/s)との比qmro／qmrkを求めよ。
(2) 低段側冷媒循環量qmro(kg/s)を求めよ。
(3) 冷凍能力Φo(kW)を求めよ。
(4) コンパウンド圧縮機の実際の駆動軸動力P(KW)を求めよ。
なにはともあれ、概略図と（線図）を描きましょう。
数値を書き加えるとウッカリミスが減るかもね。概略図もサクッと描けられれば鬼に金棒です。 目をつぶっても描けるぐらいなら合格！
(1) 低段側冷媒循環量qmro(kg/s)と高段側冷媒循環量qmrk(kg/s)との比qmro／qmrkを求めよ。
考え方は令和2年度(1)と同じ考え方です。
設問を読みこの基本式が出てくれば合格。（基本式は2冷レベル）
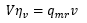
V ： ピストン押しのけ量 qmr ： 冷媒循環量 ηv ： 体積効率 v ： 比体積
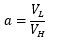
a ： 気筒数比 VL ： 低段側ピストン押しのけ量 VH ： 高段側ピストン押しのけ量
よって、設問を基本式に当てはめると
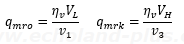となる。
比qmro／qmrkは、
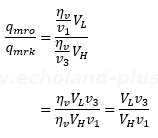
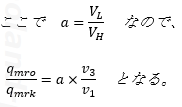
では、数値代入しましょ。
答え 0.718
(2) 低段側冷媒循環量qmro(kg/s)を求めよ。
楽勝でしょう！！
qmrkは設問で指定されています(qmrk＝0.5kg/s)し、（1）でqmro／qmrkを求めました。
よって、
qmro／qmrk ＝ 0.718
qmro／0.5 ＝ 0.718
qmro ＝ 0.718 × 0.5
＝ 0.359
答え 0.359 (kg/s)
(3) 冷凍能力Φo(kW)を求めよ。
基本式は、
Φo＝qmro(h1－h8)（← 2冷レベル）
ここで、h8が設問で指定されていませんので、求めます。中間冷却器の熱収支式を組み立てましょう。これがポイント。
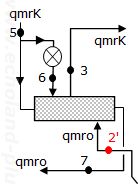
左辺に入るもの、右辺に出るものでまとめます。
qmrkh5 ＋ qmroh'2 ＝ qmrkh3 ＋ qmroh7
（h2は、h'2であることに注意）
qmroを左辺、qmrkを右辺にまとめます。
qmroh'2 － qmroh7 ＝ qmrkh3 － qmrkh5
qmro(h'2 － h7) ＝ qmrk(h3 － h5)
ハイ、qmroとqmrkを含んだ熱収支式の出来上がり。
ここで、h7を求めるには（1）と（2）の答えを利用するために、上記の熱収支式から次のように表す。
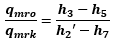
この式に与えられた数値求めた数値を代入すればh7が求められます。 （長々と記述していますが本番では余白が少ないですから、いきなりこの式を書いても良いですよ。練習してください。）
では、h'2を求めましょう。
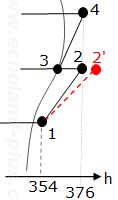
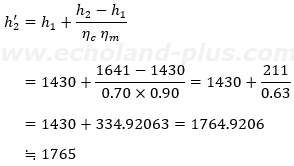
ここで、qmro／qmrkは（1）で 0.718
と求めたので、与えられた数値と一緒に熱収支式に代入します。
基本式。
Φo＝qmro(h1－h8)
ここに、h7 ＝ h8
Φo ＝ 0.359 × (1430 － 225)
＝ 0.359 × 1205
＝ 432.595
≒ 433
答え 433 (kW)
ここで、メールにて問い合わせがあったので少々追加します。（2022(R04)/02/13）
日本冷凍空調学会の模範解答は、答えが「431(kW)」となっています。
それに合うように計算してみましょう。
上記の計算では、qmro／qmrkを「0.718」としていましたが、「0.72」で計算してみます。
Φo ＝ 0.359 × (1430 － 228.9)
＝ 0.359 × 1201.1
＝ 431.1949
≒ 431
答え 431 (kW)
これで、模範解答集と同じ「431 kW」になりました。
ここで、なぜ、qmro／qmrkを「0.718」ではなく「0.72」で計算するのは、数学的なことなのか、冷凍サイクル的なことなのか、よくわかりません。また、h7は「229」で計算しても良いでしょう。（模範解答は「228.8」で計算）
1冷の学識計算では、採点者は計算過程の記述を見て、受験者がちゃんと理解しているか重点を置くと思いますので、あきらかな計算ミスで答えがズレてしまった場合でなければ、減点されないと思います。
自信を持って式を組み立てられるようにして、本番では採点者に向かって「完璧です、どうぞ間違えないように採点してください。」と、心の中で言えるように仕上げてみましょう。
なお、コマゴマと途中の計算を記述していますが、本番では大胆にカットできるよう仕上げてください。
(4) コンパウンド圧縮機の実際の駆動軸動力P(KW)を求めよ。
低段側圧縮機駆動軸動力をPL、高段側圧縮機駆動軸動力をPHとすると、
P ＝ PL ＋ PH
よって、
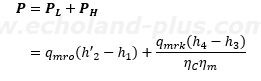
h'4は前述のh'2のように別個に求めずh4のまま組み込んで計算することにします。
では、数値代入して一気に
確認の意味で別回答
Φkを求め、以下の基本式でも求められます。308(kW)が正しいか確認してみましょう。
P ＝ Φk － Φo （← 3冷レベル）
Φk ＝ qmrk(h'4 － h5) （← 2冷レベル）
（h4は、h'4であることに注意）
ここで、h'4を求めましょ。
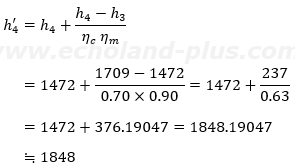
Φk ＝ qmrk(h'4－h5)
＝ 0.5 × (1848 － 366)
＝ 741
P ＝ Φk － Φo
＝ 741 － 433
＝ 308
答え 308 (kW)
コメント
（1）の気筒数比を把握しているかがポイント。（1）ができなければ、（2）も撃沈。（3）は熱収支を把握していなければh7が求められない。（4）は（1）～（3）ができれば楽勝。令和2年に続けて微妙に違いますが同様な問題でした。これは落とせない。
訂正箇所履歴
【2021(R03)/06/05 新設】
- (3)の計算式内で「＝ 0.0359 × 1205」→「＝ 0.359 × 1205」に訂正。（2022(R04)/02/13）
- (2)の計算式で、下記のマーキング箇所（0.0718）が誤植のため訂正。（2023(R05)/05/12）
qmro／qmrk ＝ 0.0718
qmro／0.5 ＝ 0.0718
qmro ＝ 0.0718 × 0.5
↓
qmro／qmrk ＝ 0.718
qmro／0.5 ＝ 0.718
qmro ＝ 0.718 × 0.5