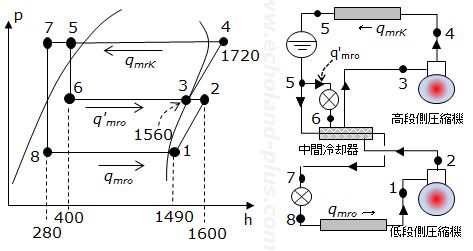
アンモニア 二段圧縮一段膨張冷凍装置
二段圧縮一段膨張の冷凍装置で特にひねったところもなく解きやすい問題です。
第一種冷凍機械責任者試験 令和5年度（11月試験）
問1 アンモニアを冷媒とする二段圧縮一段膨張の冷凍装置を下記の冷凍サイクルの運転条件で運転するとき、次の(1)から(3)の各問に、解答用紙の所定欄に計算式を示して答えよ。
ただし、圧縮機の機械的摩擦損失仕事は吐出しガスに熱として加わるものとする。また、配管での熱の出入りおよび圧力損失はないものとする。
（20点）
(理論冷凍サイクルの運転条件)
低段圧縮機吸込み蒸気の比エンタルピー h1 ＝ 1490 kJ/kg
低段圧縮機の断熱圧縮後の吐出しガスの比エンタルピー h2 ＝ 1600 kJ/kg
高段圧縮機吸込み蒸気の比エンタルピー h3 ＝ 1560 kJ/kg
高段圧縮機の断熱圧縮後の吐出しガスの比エンタルピー h4 ＝ 1720 kJ/kg
凝縮器出口の液の比エンタルピー h5 ＝ 400 kJ/kg
蒸発器用膨張弁直前の液の比エンタルピー h7 ＝ 280 kJ/kg
（実際の冷凍装置の運転条件）
蒸発器の冷媒循環量 qmro ＝ 0.125 kg/s
圧縮機の断熱効率（低段、高段とも） ηc ＝ 0.70
圧縮機の機械効率（低段、高段とも） ηm ＝ 0.85
(1) 中間冷却器の必要冷却能力 Φm（kW）を求めよ（小数点以下第1位までとする）。
(2) 凝縮器の冷媒循環量 qmrk（kg/s）を求めよ（小数点以下第3位までとする）。
(3) 実際の冷凍装置の成績係数 (COP)R を求めよ（小数点以下第2位までとする）。
なにはともあれ、概略図と線図を描きましょう。
p－h線図と、装置の概略図を書きましょう。
- qmro ＝ 0.125 kg/s
- ηc ＝ 0.70 (L,H共)
- ηm ＝ 0.85 (L,H共)
サクっと描き上げられるように何度も練習しましょう。
1種冷凍学識令和5年度問 1 二段圧縮一段膨張サイクル図とp-h線図
(1) 中間冷却器の必要冷却能力 Φm（kW）を求めよ（小数点以下第1位までとする）。
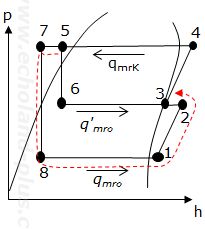
問 1 二段圧縮一段膨張p-h線図
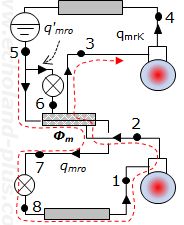
問 1 二段圧縮一段膨張サイクル図
図は理論上のp－h線図とサイクル図です。中間冷却器では、
- h6から h7へ qmroが冷却される。
- h2から h3 へ qmroが冷却される。
と、覚える。
なので、中間冷却器の必要冷却能力 Φmは
Φm ＝ qmro(h6 － h7) ＋ qmro (h2 － h3)
と、覚える。
qmroでまとめて、
Φm ＝ qmro{(h6 － h7) ＋ (h'2 － h3)}
ここで、注意） h2 は、h'2 とすること。
h'2を求めましょ。
h'2 ＝ h1 ＋ (h2 － h1) / ηcηm
＝ 1490 ＋ {(1600 － 1490) / (0.85 × 0.70)}
＝ 1490 ＋ (110 / 0.595) ＝ 1674.8739
≒ 1675
数値代入。
Φm ＝ qmro{(h6 － h7) ＋ (h'2 － h3)}
＝ 0.125 × {(400 － 280) ＋ (1675 － 1560)}
＝ 0.125 × (120 ＋ 115) ＝ 29.375
≒ 29.4 （小数点以下第1位まで）
答え Φm ＝ 29.4 (kW)
(2) 凝縮器の冷媒循環量 qmrk（kg/s）を求めよ（小数点以下第3位までとする）。
問 1 二段圧縮一段膨張p-h線図
基本式
Φm ＝ q'mro(h3 － h6)
qmrk ＝ qmro ＋ q'mro
ここに、h5 ＝ h6
q'mro ＝ Φm / (h3 － h6)
＝ 29.4 / (1560 － 400)
＝ 0.0253448 ≒ 0.025
qmrk は、
qmrk ＝ qmro ＋ q'mro
＝ 0.125 ＋ 0.025
＝ 0.150（小数点以下第3位まで）
答え qmrk ＝ 0.150（kg/s）
(3) 実際の冷凍装置の成績係数 (COP)R を求めよ（小数点以下第2位までとする）。
基本式
(COP)R ＝ Φo / P
Φo ＝ qmro(h1 － h8) ここに、h8 ＝ h7
P ＝ PL ＋ PH
PL ＝ qmro (h2 － h1) / ηcηm
PH ＝ qmrk (h4 － h3) / ηcηm
では、数値代入して一気に。
Φo ＝ qmro(h1 － h8)
＝ 0.125 × (1490 － 280)
＝ 151.25 ≒ 151
PL ＝ qmro (h2 － h1) / ηcηm
＝ 0.125 × (1600 － 1490) / 0.70 × 0.85
＝ 0.125 × (110 / 0.595)
＝ 23.109242 ≒ 23.1
PH ＝ qmrK (h4 － h3) / ηcηm
＝ 0.150 × (1720 － 1560) / 0.70 × 0.85
＝ 0.150 × (160 / 0.595)
＝ 40.336134 ≒ 40.3
P ＝ PL ＋ PH
＝ 23.1 ＋ 40.3 ＝ 63.4
(COP)R ＝ Φo / P
＝ 151 / 63.4 ＝ 2.3817034
≒ 2.38 （小数点以下第2位まで）
答え (COP)R ＝ 2.38
ポイント
- 中間冷却器の必要冷却能力 Φmが導くことができれば、あとは2冷レベルなので大丈夫でしょう。
ご健闘をお祈りします。
訂正箇所履歴
【2024(R06)/01/20 新設】
- (1)の計算式で、h'2であるべきところがh2表記だったので訂正。（赤字部分）（2024(R06)/04/24）