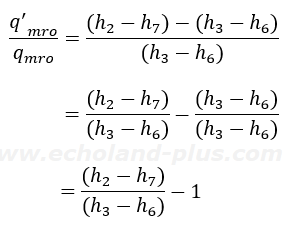1種冷凍学識計算攻略-問1：多段圧縮のポイント
EchoLand-plus
熱収支を左辺と右辺にまとめるべし、その前にやることがある。
問1の多段圧縮冷凍装置の問題を解くカギは熱収支（ヒートバランス）を読み解くことです。それには、熱の出入りを考えなければなりません。その前にやっておくことがあります。それは、まず下図の線図を覚えることです！
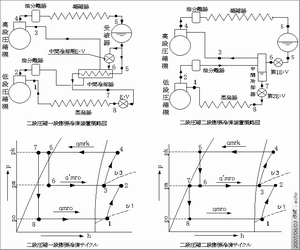
下記の図は平成10年5月31日の第一種冷凍機械講習検定問題の問題1です。一段膨張方式と二段膨張方式の概略図とp-h線図があります。 この問題は、この両方の装置を説明するのにもってこいの問題です。（多段圧縮冷凍装置の原理やp－h線図の説明は省略します。一種冷凍機械責任者用のテキストを読んでください。）
第一種冷凍機械講習検定問題 問題1 （平成10年5月31日）
問1 次の図は、一段膨張方式および二段膨張方式による二段圧縮冷凍装置の各膨張方式の概略図とp-h線図上の冷媒の各状態点における比エンタルピーh1～h6、低段圧縮機冷媒循環量qmroおよび中間圧力pmは、いずれの膨張方式でも同じ値である。また、比エンタルピーh7、h8並びにバイパス冷媒循環量q'mroと高段圧縮機冷媒循環量qmrkは、膨張方式によって異なる値である。
これらの両膨張方式による冷凍装置の理論冷凍サイクルについて、次の（1）～（4）の各問に答えよ。
（1） 冷凍サイクルの冷凍能力Φoを表す式を示せ。
（2） 冷凍サイクル内の冷媒流量比q'mro／qmroおよびqmrk／qmroを表す式を示せ。
（3） 断熱圧縮動力Pthを表す式を示せ。
（4） 上記の（1）、（2）および（3）で表した各式から、二段膨張方式のほうが一段膨張方式よりも Φo、q'mroおよびPthの値が若干大きくなる理由を簡単に述べよ。
その前にやる事とは
この2種類の概略図とp-h線図を記憶してください。二段圧縮一段膨張方式と二段圧縮二段膨張方式をノートにガンガン書いてください。 これから先、外略図だけ、線図だけ、文章だけと、いろいろな問題がでてきます。
そのときに、自由自在に概略図とp-h線図を書くこと ができるように、ドンドン、ガンガン、ノートに書いてください。（勉強していれば自然に書くことができるようになると思いますが・・・・）
（1）冷凍サイクルの冷凍能力Φoを表す式を示せ。
軽くこなします。
Φo ＝ qmro（h1 － h8） ですね。
一段膨張も二段膨張もまったく同じ式です。
（2） 冷凍サイクル内の冷媒流量比 q'mro／qmro および qmrk／qmro を表す式を示せ。
冷媒流量を求めることが、この問題全体のポイントです。
問題集の解説文やテキストに、いきなり出てくる式はこんな感じです。
中間冷却器の冷媒の流入と流出の熱収支を表すと、
この式の意味わかります?どうやって導き出してきたのでしょう。p－h線図を見るとな～んとなく分かるような感じですが・・・・私の場合チンプンカンでした。 なので、この式を記憶したのでした。でも、結局、だめでした…、少しひねられた問題になると分からなくなってしまうのです。 応用が利かないのです。
でも、この式を導き出す良い方法を発見?したのです。 ぇ～、念を押しておきますけど、これは私（echo）にとっては良い方法ということですから…、その辺よろしく。
◆ 考え方としては、中間冷却器の熱収支を分かりやすくまとめるということです。
それでは、二段圧縮一段膨張冷凍装置と二段圧縮に断膨張方式の中間冷却器の部分だけを抜き取った図を書いてみます。 貴方もぜひ、ノートに書いてください。
適当に語句は、省いてガンガン書いてください。
でも、●点と数字はp-h線図と照らし合わせて書いてください。 それと、冷媒の流れる向きや種類（qmroとかqmrkとか）は重要ですからは省かないで。
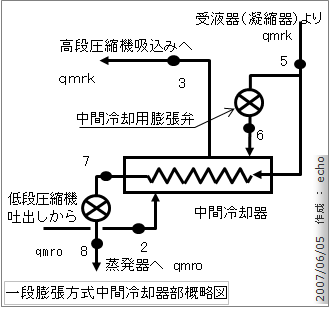
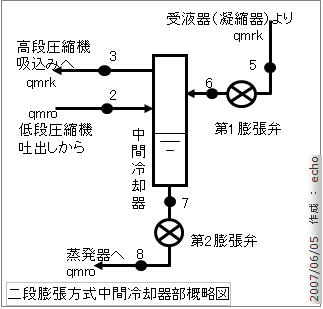
「一段膨張方式」と「二段膨張方式」の中間冷却器概略図はサクッと！描けるようになれば最高Maxです。
◆ 中間冷却器の熱収支を見てみます。上の図から、中間冷却器に「入るもの」と「出るもの」を抜き出してみましょう。
どれも、冷媒循環量と比エンタルピーをセット（積）で抜き出してみます。
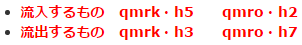
これです、これ! これが、二段圧縮冷凍装置（熱交換器）の問題を解くカギになります。
ここで、
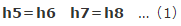
（1）式を頭に入れてください。この辺は理解していますよね、5の点と6の点（7と8）はエネルギー（比エンタルピー）は同じってことです。 この辺は二段膨張方式の第1膨張弁あたりを見るとなんとなく分かってくると思います。一段膨張方式も二段膨張方式も同じ式になります。とにかく、同じなんです。
よく分からない方はp-h線図も見ながら考えてください。
◆ 次に、流入するものを左辺に、流出するものを右辺にまとめます。
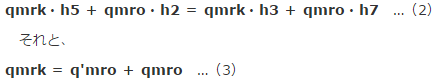
（1）（2）（3）式のを組み合わせれば、もう怖いものなしという気がしませんか。流入するもの流出するもの、比エンタルピーの大きさ、それと冷媒流量の関係、OKですか?
この3つの式が一番の基本です。 この式を出すためには、概略図とp-h線図を書くことができればすぐに導き出せます。 試験時間を有効に使えます。そして、問2のホットバイパス装置や液ガス熱交換器にもこの考え方応用できます。
この考え方は電気で言えば「キルヒホッフの方式」に似ているような気がします。（後述）
◆ さて、（2）式を元にして問題を解いてみましょう。
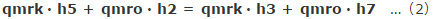
＜＜元画像＞＞
となりました。
ぅ～む、中学校の数学の授業のようですね。冷凍機械責任者試験は、＋ － × ÷ の四則演算しか出現しません。
この式は、一番最初にできてきた。
中間冷却器の冷媒の流入と流出の熱収支を表すと、
と、同じです。（2）式からこの式が導き出せたのです。めでたしめでたし！
さて、（２）で問うているのは、
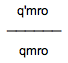ですから、
上記の式、qmro［(h
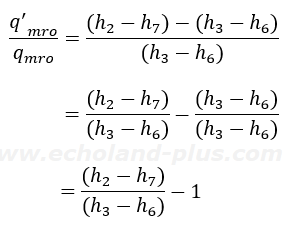
もう一つは
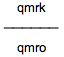です。
これは、先に（↑上の方で）qmrkとqmroをまとめたときの式を使います。
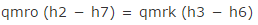から、
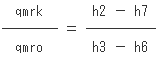と、なります。
楽勝ですね!
ここで、答案用紙には長々と式を書くと場所がなくなってしまいます（たぶん）、それと時間もかかるでしょう。なので、メモ欄の部分に 一度、大ざっぱに書いてから解答欄にまとめた式を書けばよいと思います。出題者が何を望んでいるか考えます。
この場合は、 ズバリ中間冷却器の熱収支が理解できているかです。
（2）の解答のまとめ
解答用紙に書ききれなくならないため、上記の説明をザクっとまとめてみます。
中間冷却器の熱収支を表すと、
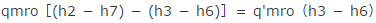
よって、
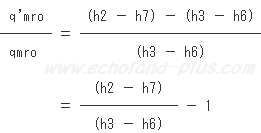
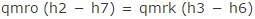で、あるから
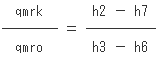
こんな感じで如何でしょうか。さぁ、ガンガン、ドンドン、問題を解きましょう。
（3） 断熱圧縮動力Pthを表す式を示せ。
この問題はサービスと言ってもいいでしょうか、ま、（4）の問いのためなんですけどね。 低段側と高段側の冷媒循環量と比エンタルピーが与えられているので、二種冷凍のときの覚えた公式（別窓で開きます）をそのまま使えばよいでしょう。
低段側の断熱圧縮動力と高段側の断熱圧縮動力を足せばいいですね。
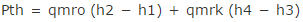
ところが、これだけだと満点をもらえないかもしれません。なぜかって、綺麗な式じゃないから！ぃぇ、ぃえ、…たぶん、最後の（4）のPthの比較問題に係わってくるからです。
どうするかっていうと、（2）で導き出した式を使います。
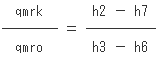から、
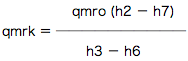
なので、
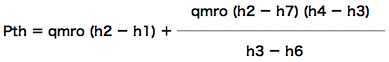
と、まぁこんな具合に、qmroと比エンタルピーの式にまとめます。（この式で、（4）の問題を解いていきます。）
（3）の解答のまとめ
Pth ＝ qmro (h2 － h1) ＋ qmrk (h4 － h3)
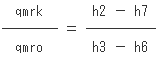であるから、
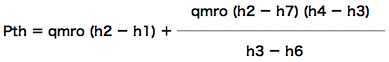
他にいろいろと書かなくても、これでいいと思う。
（4） 上記の（1）、（2）および（3）で表した各式から、二段膨張方式のほうが一段膨張方式よりも Φo、q'mroおよびPthの値が若干大きくなる理由を簡単に述べよ。
この問題で一段膨張と二段膨張の違いが分っているか試されます。一段と二段のp-h線図から、異なる部分をを抜き出してみます。
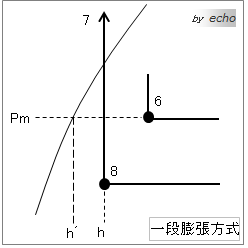
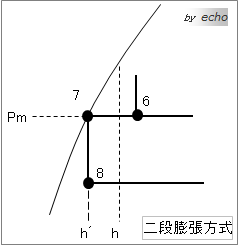
h´とhの違い、分かります？ h´＜ h ということです。
つまり、
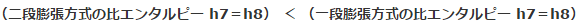＜＜元画像＞＞
なので、蒸発器入口の比エンタルピーh8は二段膨張方式のほうが小さいのです。
これは、一段の場合は中間冷却器の伝熱管の熱伝達抵抗により中間圧力Pmでの飽和温度まで冷却できない、と、いうことらしいです。さて、これで（4）の問題がスラスラ解けるはず…、です。
さ、いきなりまとめてしまいましょう。
（4）の解答のまとめ
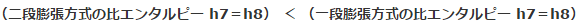…（1）
＜＜元画像＞＞
・Φo（冷凍能力）
Φo ＝ qmro (h1 － h8)
（1）より、二段膨張方式のほうが一段膨張方式よりもΦoの値が若干大きくなる。
・q'mro
中間冷却器の冷媒の熱収支は、
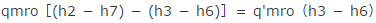
よって、
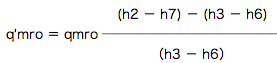で、あるから
（1）より、二段膨張方式のほうがq'mroの値が若干大きくなる。
・Pth
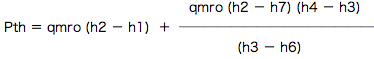であるから、
（1）より、二段膨張方式のほうがPthの値が若干大きくなる。
ぅわ～、チョと長いですかね。（1）～（3）の式に番号を付けてその番号だけ書いても良いかもしれません。そういう切り替えがサクッとできるのは やはり、過去問を数多くこなしてないとできないかもしれません。
このページもだいぶ長くなってしまいました、一段膨張方式と二段膨張方式の違いが分かりましたでしょうか。ま、違いが分からなくても、 中間冷却器の熱収支の式の導き出し方と、線図と概略図を書く事ができればＯＫ牧場！
次ページの「問1：熱収支攻略」で熱収支攻略をしましょう。一段膨張方式と二段膨張方式の過去問でどんな問題が出題されているか見てみましょう。 全科目試験（11月）と、講習検定試験の過去問題をまとめてあります。
訂正箇所履歴
【2016(H28)/10/22 新設】
- 計算式がスマホなどで崩れるため、自動で大きさが変化する画像にした。少々、文を見直し。（2017(H29)/03/31）
- 問い合わせがあったため、下記式の途中変形を追加。（2023(R05)-05-07）
↓ （式の途中変形を追加）