2種冷凍学識計算攻略-基礎
EchoLand-plus
全般的な基礎知識を求められる問題は結構つらいです。
いままでに、冷媒循環量qmr、冷凍能力Φ、軸動力P、成績係数COPなど基礎的な式で解答する問題がありました。
式を丸覚えでこれまでの問題が解ければ、とりあえずは1問は正解かも知れません。 しかし、このページに掲げる過去問のように、さらに基礎的な知識、前ページでの圧縮機吐出しガス比エンタルピーの問題が、さりげなく出題される年度があるので注意が必要なのです。
前ページまでの集大成的な問題
機械損失仕事は熱として冷媒に「加わらない」「加えられる」の実践問題です。 それから、前ページまでの知識が必要になります。頑張ってください。
平成13年問1 さりげなく出題、圧縮機吐出しガス比エンタルピー
この問題は今までと違い、イ．からハ．まで○か×か問われる問題です。むしろ簡単かも知れませんが、落とし穴に落とされないようにしましょう。
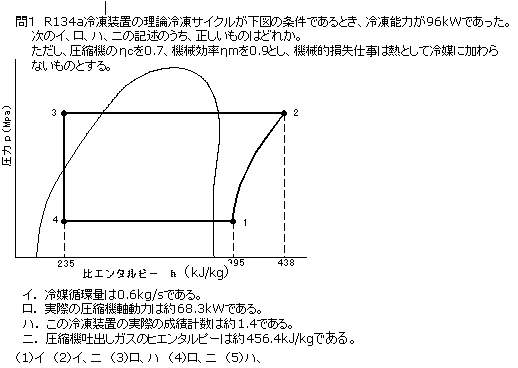
指定されている値を拾い出してみます。
- 冷凍能力 Φo＝96 ［kW］
- 断熱効率 ηc＝0.7
- 機械効率 ηm＝0.9
- 比エンタルピー h4＝235 ［kJ/kg］
- 比エンタルピー h1＝395 ［kJ/kg］
- 比エンタルピー h2＝438 ［kJ/kg］
一つずつじっくり解いてみましょう。
まずはイ．から、冷媒循環量qmrを求めるには・・・・
上記の値をザ?っとみて思い浮かべてください。ハイそうですね、（2）式！
Φo ＝ qmr (h1 ─ h4) .....（2）式を、変形して
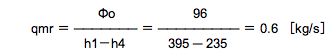
よって、イ．の0.6［kg/s］は【正しい】
イ．で冷媒循環量qmrが求められたので、軸動力Pの公式
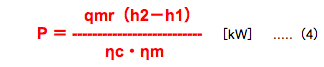
式を使って計算してみましょう。
「機械損失仕事は熱として冷媒に加わらないものとする。」とありますが、勘違いしないように。前ページで学んだように動力の計算は機械効率ηmも入れてくださいね。
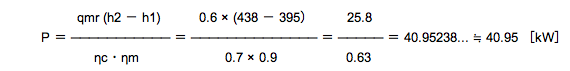
よって、ロ．の約68.3kWは【誤り】です。
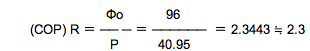
もう一つの計算式で確かめてみます。
(COP)R ＝ {(h1 － h4) / (h2 － h1)}ηcηm
＝ {(395 － 235) / (438 － 395} × (0.7 × 0.9)
＝ 3.7209 × 0.63 ＝ 2.344167
≒ 2.3
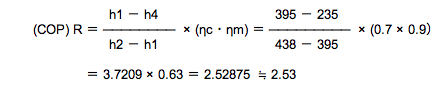
よって、ハ．の約1.4は【誤り】
このように、h1、h2、h4とηc、ηmが分かっていれば実際の成績係数COPを求めることができますから、 2つの公式で答えの確認もできます。
わからない人は「成績係数（COP）攻略」を勉強してみてください。ΦoとPで成績係数を求めた場合、イ．やロ．でミスるとすべてがパーになってしまいますから注意が必要です。
実際の圧縮機吐出しガス比エンタルピーをh2´とすると、問題文に「機械損失仕事は熱として冷媒に加わらないものとする。」 とありますから、ηmを外して計算します。前ページの
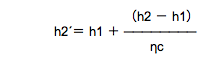
.....（8）式で、計算します。
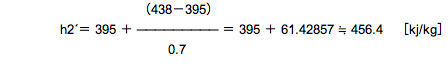
ニ．は【正しい】というわけです。
正解は （2）イ、ニ となります。
平成18年問1 上記の平成13年と類似した問題です、さぁ、じっくり料理してください。
まずは、問題文をよ～く読んでください。大きく違うところは・・・、続きは問題画像の下に書きましょう。
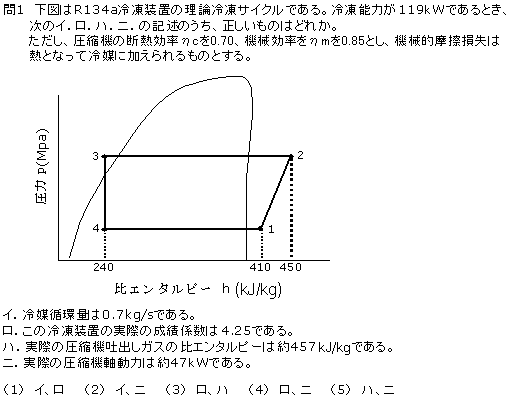
そうです、「機械的摩擦損失仕事は熱となって冷媒に加えられるものとする。」なのです。13年とこの年の問題をクリアして、怖いもの無し! さぁ、頑張ろう。
では、指定されている値を拾い出してみましょう。
- 冷凍能力 Φo＝119 ［kW］
- 断熱効率 ηc＝0.7
- 機械効率 ηm＝0.85
- 比エンタルピー h4＝240 ［kJ/kg］
- 比エンタルピー h1＝410 ［kJ/kg］
- 比エンタルピー h2＝450 ［kJ/kg］
上記の平成13年の問題のように、軸動力を求めてから成績係数と進むのが普通？ですが、この問題は、ゥ～む、いきなり問ハの成績係数を求めよとなります。
ま、…比エンタルピーが分かっているので、そうです。その式です。(6)式です。
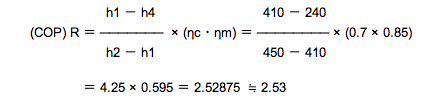
よって、ロの4.25は【誤り】
いいですかぁ。4.25は（ηc・ηm） を無視した計算結果ですよぉ。つまり、理論成績係数のことです。
意味のわからない人は「成績係数（COP）を求める問題を攻略する。」を勉強してみてください。
「機械的摩擦損失仕事は熱となって冷媒に加えられるものとする。」とあるので、平成13年の 問題と混同しないようにしてください。 ま、素直に?考えれば良いんでしょうけど。
ηm（機械効率）を含めて計算します。（上記の平成13年のニ.の問題と、比べてみてね）
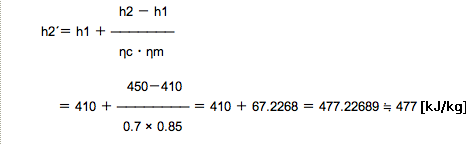
よって、ハの約457kJ/kgは【誤り】になります。
ちなみに、0.85（ηm）だけで計算すると、457が計算結果になります、わざわざηcをはずしてηmだけで計算しないと思いますが…。
これは、素直に解けばいいでしょう。問題の意図としては…（ηc・ηm）を入れて計算するかどうかあなたは出題者に挑戦されていると云うことでしょう。もちろん、イ.の冷媒循環量が求められていることが前提です。
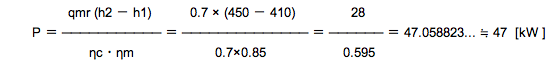
よって、ニ．の約47kWは【正しい】です。
平成15年問2 基礎の基礎まで突っ込まれる問題
この問題は、けっこうややこしくてつらいです。近年（?平成22年度）は、緩和のせいなのか素直な問題が出題され、下記のよような問題はありません。が、油断は禁物と云ったところでしょうか。
下記の問題では、具体的な数値はいっさい出てきません。公式だけの展開を要求されます。 さらに、基礎的なことも出題され、公式丸覚えで今までなんとか解いてきたのですがそれだけではすまないといった感じです。
力試しで一度解いてみても時間の無駄にはならないでしょう。
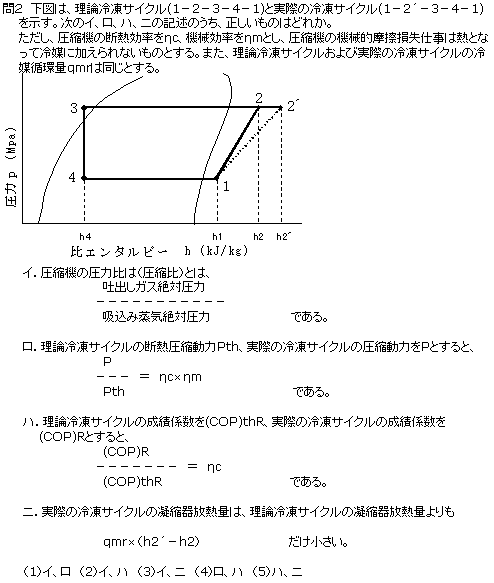
チョイと整理してみます。
- 理論冷凍サイクル １－２－３－４
- 実際の冷凍サイクル １－２´－３－４
- 断熱効率 ηc
- 機械効率 ηm
- 蒸発器入口比エンタルピー h4
- 圧縮機吸込み蒸気比エンタルピー h1
- 理論圧縮機吐出し蒸気比エンタルピー h2
- 実際の圧縮機吐出し蒸気比エンタルピー h2´
- （圧縮機の機械的摩擦損失は熱となって冷媒に加えられない）
- 理論冷媒循環量と実際の冷媒循環量は共に（qmr）同じ
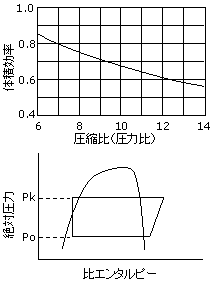
学識はわりと計算問題ばかりに気を取られがちですがこのような基礎的なことがさらりと出題されます。
右図のグラフは体積効率と圧力比の関係を示したもので、圧力比が大きいほど体積効率は小さくなります。 圧力比から体積効率を求めなければならないという問題もあります（1冷平成12年）。
圧縮機吸込み絶対圧力 Po
圧縮機吐出し絶対圧力 Pk と、すると
イ.の答えは【正しい】
ここで、絶対圧力に注意してください。
絶対圧力 ＝ ゲージ圧力 ＋ 0.1 ［Mpa abs］
p-h線図の縦軸は絶対圧力ですからそのまま読み取ればいいのですが、問題文に圧力計の指示値などと書かれていたらゲージ圧力になりますので、0.1をプラスして絶対圧力の値で表なりグラフなりから読み取らなければなりませんし、計算だけの場合もゲージ圧力のままで計算すると答えが違ってしまいます。
前ページで機械効率ηmについて書きましたが、もう一回断熱効率ηcと共に考えてみましょう。
- 理論断熱圧縮動力 Pth ［kW］
- 実際の圧縮機の駆動に必要な軸動力 P ［kW］
- 蒸気の圧縮に必要な動力 Pc ［kW］
- 機械的摩擦損失動力 Pm ［kW］
と、すると、
に、なります。
ここで、ηc × ηmを全段熱効率（ηtad）といいます。
上記の関係式から、
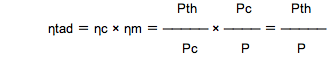
よって、ロ.は【誤り】 （PthとPが逆です）
全段熱効率ηtad（ηc×ηm）は、理論断熱圧縮動力Pthと実際の所要軸動力Pの比です。
冷媒循環量qmrは理論と実際が同じであるから、（5）、（6）式から
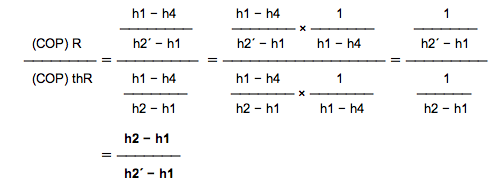
ここで、h2´は
圧縮機の機械的摩擦損失は冷媒に熱となって加えられないとあるから
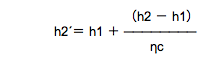
h2´を代入すると、
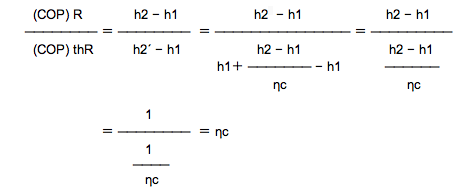
ハ.は【正しい】
ぅ～む、まるで数学か算数のテストみたいです。引っ掛けに注意しながら式の展開うっかりミスにも気を付けましょう。
（最後の式の分子h2´→ h2 に、変更（記載ミス）しています。2015（H27）年5月30日記す。）
問題は基礎の基礎まで突っ込んできます。ここで、凝縮器放熱量（凝縮負荷とも言います）を考えてみます。
- 理論冷凍サイクル １－２－３－４
- 実際の冷凍サイクル １－２´－３－４
- 凝縮器出口蒸気比エンタルピー h3
- 理論圧縮機吐出し（凝縮器入口）蒸気比エンタルピー h2
- 実際の圧縮機吐出し（凝縮器入口蒸気比エンタルピー h2´
- 理論冷媒循環量と実際の冷媒循環量は共に（qmr）同じ
凝縮放熱量（凝縮負荷）実際をΦkを、理論値Φthkとすると、
- Φk ＝ qmr（h2´－h3）
- Φthk ＝ qmr（h2－h3）
凝縮負荷は、（凝縮器冷媒循環量qmr）×（凝縮器の入口(h2)と出口(h3)の比エンタルピー差 ）ってこと、冷凍能力Φoと同じ考え方です。
で、問題は、Φk － Φthk は、どうなるかってことですから、
なので、qmr (h2´－ h2) だけ大きいということですから、小さいと云っているニ.は【誤り】となります。
次のページで、2種学識計算攻略は終わりです。熱計算は近年（2011年03月15日記）出題されていません。さて、どうしましょう。と云うページにまります。
訂正箇所履歴
【2017/10/11 新設】
- ニ．の計算式が全然違っていたので訂正。（2017/10/11）
↓
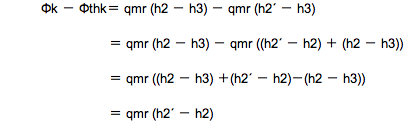
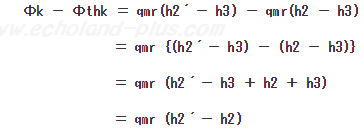
↓再度訂正（ ＋ h2 → － h2）
- 問1のハ．の下記の計算式答えが間違っていたので訂正。（2024(R06)/10/14）
↓
(COP)R ＝ {(h1 － h4) / (h2 － h1)}ηcηm
＝ {(395 － 235) / (438 － 395} × (0.7 × 0.9)
＝ 3.7209 × 0.63 ＝ 2.344167
≒ 2.3